Approximate nearest neighbor search with DiskANN in libSQL

Vector search queries for huge datasets of large embeddings for retrieval-augmented generation require approximate nearest neighbor (ANN) search to meet the scale, as discussed in the previous blog post on RAG and vector search. Today, we will explore how we implemented the DiskANN algorithm in the libSQL to meet these needs.
#Exact nearest neighbor search
In the previous blog post, we ended with an exact nearest neighbor search example with a movies table:
-- create table with F32_BLOB vector column
CREATE TABLE movies (
title TEXT,
year INT,
embedding F32_BLOB(3)
);
-- insert data
INSERT INTO movies VALUES ('Raiders of the Lost Ark', 1981, vector('[1,2,3]'));
INSERT INTO movies VALUES ('Indiana Jones and the Temple of Doom', 1984, vector('[1,2,4]'));
INSERT INTO movies VALUES ('Indiana Jones and the Last Crusade', 1989, vector('[1,2,5]'));
INSERT INTO movies VALUES ('Indiana Jones and the Kingdom of the Crystal Skull', 2008, vector('[5,6,7]'));
INSERT INTO movies VALUES ('Indiana Jones and the Dial of Destiny', 2023, vector('[5,6,8]'));
-- find 3 exact nearest neighbors
SELECT title, year FROM movies ORDER BY vector_distance_cos(embedding, vector('[5,6,7]')) LIMIT 3;
Although the last query returns exact results, the problem is it has to scan through all the rows in the table. This means that the I/O and CPU overhead for exact search grows linearly with table size, which is usually unacceptable for medium and large datasets.
#Approximate nearest neighbor search
ANN search trades accuracy for speed and can return just close enough candidates instead of exact nearest neighbors. Usually, the N-recall@K metric is used to estimate quality of ANN algorithms, which is defined as the proportion of top-N exact candidates returned in the top-K approximate candidates. For example, if 1-recall@100 for an ANN algorithm equals 0.9, then for 90% of queries we will get the exact nearest neighbor in the top-100 approximate neighbors.
There are many different approaches to ANN search (locally-sensitive hashing, space partitioning, hierarchical navigable small world, to name a few; check out this in depth tutorial from CVRP2020 for more details). In this article we will concentrate on graph-based algorithms which aim to build a graph in a way that its traversal can find approximate nearest neighbors quickly by visiting only small subgraph of the whole dataset.
For vector search in libSQL, we implemented the LM-DiskANN algorithm (Pan, 2023), a low-memory footprint variant of the DiskANN vector search algorithm (Subramanya, 2019 and Singh, 2021), and integrated it into the SQLite indexing system.

For the example movies table, what you need to do to enable approximate search is first to create a vector index:
CREATE INDEX movies_idx ON movies ( libsql_vector_idx(embedding, 'metric=cosine') );
The CREATE INDEX SQL statement creates a DiskANN index movies_idx on the embedding vector column of the movies table, using the cosine distance function (1 - cosine similarity) to determine nearest neighbors.
Under the hood, in the SQLite code generator, we emit a special OP_OpenVectorIdx virtual machine bytecode instruction when we detect a vector index in a column. The instruction opens a vector index, which adds a special-case to the OP_IdxInsert instruction, which is used to update an index. In other words, when you insert a row in a table with a vector column, SQLite core calls into the DiskANN code to update the vector index. You can see these details in action in the EXPLAIN output for the INSERT statement for a table with vector index:
libsql> EXPLAIN INSERT INTO movies VALUES ('Raiders of the Lost Ark', 1981, vector('[1,2,3]'));
addr opcode p1 p2 p3 p4 p5 authors comment
---- ------------- ---- ---- ---- ----------------------- -- -------------
...
2 OpenVectorIdx 1 5 0 k(2,,) 0 (!) new opcode - opens vector index movies_idx
...
13 PureFunc 2 11 6 libsql_vector_idx(-1) 32 prepare data (libsql_vector_idx under the hood just returns its first argument)
14 IntCopy 1 7 0 0 prepare rowid
15 MakeRecord 6 2 5 0 prepare record for vector index
...
17 IdxInsert 1 5 6 2 16 insert record (vector, rowid)
...
#DiskANN
DiskANN is a graph-based approximate nearest neighbor search algorithm that scales to large amounts of data while retaining high recall. The LM-DiskANN variant of the algorithm we implemented is designed for low memory consumption by keeping only a small part of the vector index in memory while remaining efficient in search operations.
Both algorithms build a generalized sparse neighborhood graph (GSNG) for the vectors dataset, aiming to construct the neighborhood of every node so that it contains sufficiently close candidates while also preserving some distant candidates (this allows traversal algorithms to quickly jump over vector space regions). It's important to note that almost all graph operations will require not only neighbors' identifiers, but also their vectors. This is where the difference lies between original DiskANN and LM-DiskANN algorithms. DiskANN stores the graph on SSD but also stores compressed representations of all dataset vectors in-memory, while LM-DiskANN introduces a redundancy in the on-disk node format by storing both the graph and compressed neighbors on disk. So essentially, the LM-DiskANN algorithm trades memory usage for an increase in storage.
More precisely, every vector in the index is stored on disk as a fixed-size binary block (for example, the LM-DiskANN suggests using 4 KB blocks to store nodes). Each block contains data about the node identifier and its uncompressed vector data, as well as storing neighbors' identifiers with corresponding compressed vectors. With this layout, all LM-DiskANN algorithm steps can make local decisions by inspecting only a single node block, as it already has all neighbors' identifiers (to put them in a queue for further processing) and compressed vectors, which allows the detection of close neighbors to the query vector without any additional I/O.

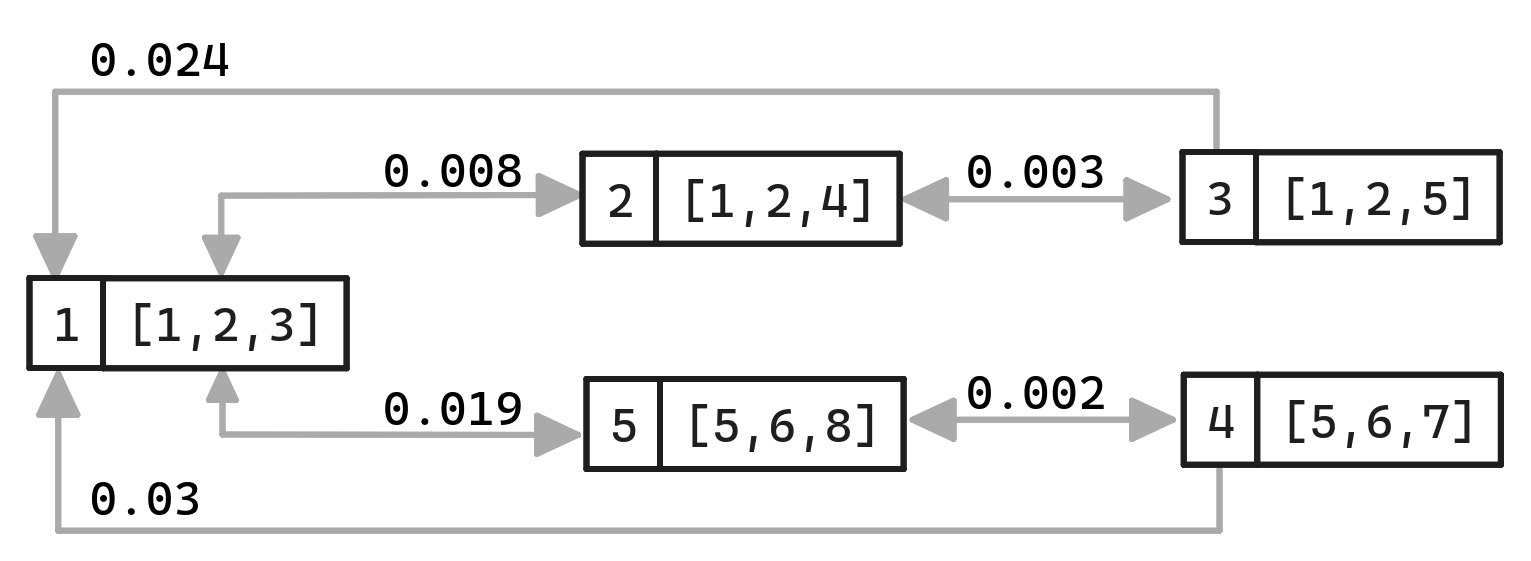
To search the vector index, libSQL provides a vector_top_k virtual table, which allows you to perform a top-k approximate nearest neighbor search to find the row IDs. You can combine the vector_top_k virtual table with a JOIN to retrieve data from the table or simply use the IN operator over the vector_top_k results. For example, to find the top 3 approximate nearest neighbors for query vector [4, 5, 6], you would do the following:
SELECT title, year FROM movies WHERE rowid IN vector_top_k('movies_idx', vector('[4,5,6]'), 3);
-- or alternatively
SELECT title, year FROM vector_top_k('movies_idx', vector('[4,5,6]'), 3) JOIN movies ON movies.rowid = id;
The way DiskANN search works is by starting from a random node and then traversing through node neighbors iteratively using Best First Search, as shown by Algorithm 1 in (Pan, 2023):

The algorithm has a configuration option L — the candidate set size. This option determines the maximum number of nodes the search algorithm considers as a potential nearest neighbors. However, the algorithm may scan more nodes than L if it starts from a node very close to the query vector. The candidate set initially consists of the random entry point vector in the graph. In each iteration, the algorithm picks the nearest candidate node, marks it as visited, and then adds all the neighbors of the visited node in the candidate set. The algorithm also prunes the candidate set to L elements, ensuring that only the closest candidates are kept in the set.
Even as the algorithm starts from a random node, you can see that after a few iterations, the algorithm will likely discover nodes in the graph close to the query vector. And as the algorithm iterates more, it will converge on the approximately nearest neighbors.
#Future
One cool thing happening right now in vector search is the emergence of binary vector representation, where instead of storing a floating point value per vector dimension, you get away with just one bit. For example, a 512-dimensional vector requires 2 KiB of space with 32-bit floating point values, which is a lot. With 1-bit representation, you only need 64 bytes!
We already have some basic plumbing in place for 1-bit vector representation. It's mostly transparent to the applications, except for index creation where you specify Hamming distance instead of cosine distance in metric index parameter:
CREATE INDEX movies_idx ON movies ( libsql_vector_idx(embedding, 'metric=hamming') );
That's because once you compress your vectors into bit-strings, cosine distance no longer makes much sense. Instead, you typically determine vector distance using Hamming distance. You also want the LLM-generating embeddings to be aware of 1-bit representation for best results.
A small footprint is also beneficial if you are running LLMs on user devices such as mobile phones. Running SQLite on the same device to provide RAG allows you to build various applications, such as AI assistants or productivity apps, that need to access privacy-sensitive, user-specific data.
#Summary
Scaling vector search to many embeddings requires us to trade off accuracy for speed by using an approximate nearest neighbor search instead of an exact search. DiskANN is a disk-based algorithm designed for this purpose. In libSQL, the DiskANN algorithm is hooked into the SQLite indexing system, automatically updating the vector index. The vector_top_k virtual table can look up rows with a similar vector from the index. In future work, we can improve DiskANN performance by compressing the index using, for example, 1-bit quantization.
#References
Suhas Jayaram Subramanya et al (2019). DiskANN: Fast Accurate Billion-point Nearest Neighbor Search on a Single Node. In NeurIPS 2019.
Aditi Singh et al (2021). FreshDiskANN: A Fast and Accurate Graph-Based ANNIndex for Streaming Similarity Search. ArXiv.
Yu Pan et al. (2023). LM-DiskANN: Low Memory Footprint in Disk-Native Dynamic Graph-Based ANN Indexing. In IEEE BIGDATA 2023.